🎉 Dimensionality Reduction: PCA vs t-SNE
🎉 Introduction to Dimensionality Reduction
Dimensionality reduction is a critical technique in data science, particularly when dealing with high-dimensional datasets. It involves reducing the number of random variables under consideration by obtaining a set of principal variables. This process not only simplifies the data but also helps in visualizing and interpreting complex datasets. Two of the most popular dimensionality reduction techniques are Principal Component Analysis (PCA) and t-Distributed Stochastic Neighbor Embedding (t-SNE). Each method has its unique strengths and weaknesses, making them suitable for different scenarios.
High-dimensional data often contains redundant or irrelevant features that can obscure meaningful patterns. By reducing the dimensionality, we can focus on the most important features, thereby improving the performance of machine learning models. Dimensionality reduction techniques like PCA and t-SNE are widely used in various fields, including image processing, natural language processing, and bioinformatics. Understanding the differences between these methods is crucial for selecting the right tool for a given problem.
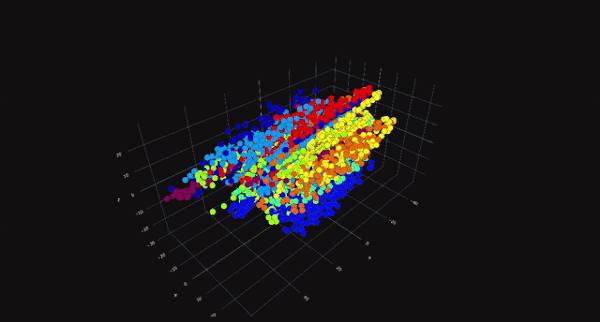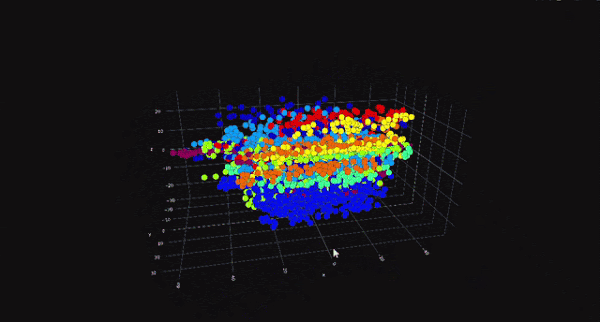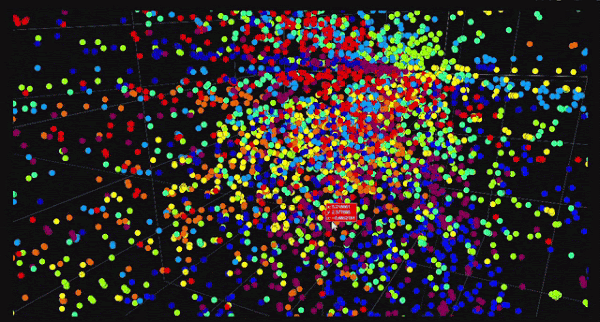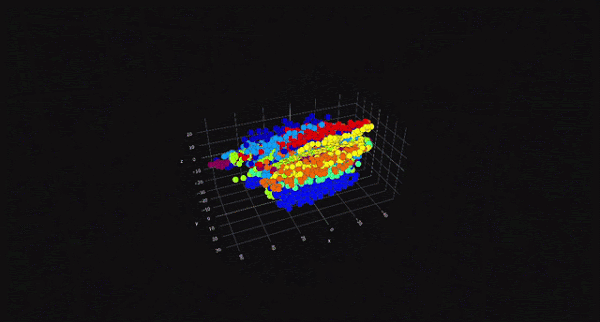
PCA is a linear dimensionality reduction technique that projects data onto a lower-dimensional space while preserving as much variance as possible. It is particularly useful for datasets with linear relationships between features. On the other hand, t-SNE is a non-linear technique that focuses on preserving the local structure of the data, making it ideal for visualizing high-dimensional data in two or three dimensions. While PCA is computationally efficient and works well for large datasets, t-SNE is better suited for exploratory data analysis and visualization.
The choice between PCA and t-SNE depends on the specific requirements of the task at hand. For instance, if the goal is to reduce dimensionality for a machine learning model, PCA might be the better choice due to its computational efficiency. However, if the objective is to visualize clusters or patterns in the data, t-SNE would be more appropriate. Both techniques have their place in a data scientist's toolkit, and understanding their differences is key to making informed decisions.
In the following sections, we will delve deeper into the workings of PCA and t-SNE, compare their strengths and weaknesses, and explore their applications in various domains. By the end of this article, you will have a comprehensive understanding of these two powerful dimensionality reduction techniques and how to apply them effectively in your data science projects.
🔍 Principal Component Analysis (PCA)
Principal Component Analysis (PCA) is a widely used linear dimensionality reduction technique that transforms high-dimensional data into a lower-dimensional space while preserving as much variance as possible. The goal of PCA is to identify the directions (principal components) in which the data varies the most and project the data onto these directions. The first principal component captures the most variance, the second principal component captures the second most variance, and so on.
PCA works by computing the covariance matrix of the data and performing eigenvalue decomposition to identify the principal components. These components are orthogonal to each other, meaning they are uncorrelated. By selecting a subset of the principal components, we can reduce the dimensionality of the data while retaining most of the information. This makes PCA particularly useful for tasks like feature extraction, noise reduction, and data compression.
One of the key advantages of PCA is its computational efficiency. It is a deterministic algorithm that can be applied to large datasets with relatively low computational cost. Additionally, PCA is easy to implement and interpret, making it a popular choice for dimensionality reduction. However, PCA has some limitations. It assumes that the data is linearly related and may not perform well on datasets with non-linear relationships. Furthermore, PCA is sensitive to the scaling of the data, so it is important to standardize the data before applying PCA.
Despite its limitations, PCA is a powerful tool for dimensionality reduction and has been successfully applied in various fields. For example, in image processing, PCA is used for face recognition and image compression. In bioinformatics, PCA is used to analyze gene expression data and identify patterns. In finance, PCA is used for risk management and portfolio optimization. By reducing the dimensionality of the data, PCA helps to simplify complex datasets and uncover hidden patterns.
In summary, PCA is a versatile and efficient dimensionality reduction technique that is well-suited for datasets with linear relationships. It is particularly useful for tasks that require feature extraction, noise reduction, and data compression. However, for datasets with non-linear relationships, other techniques like t-SNE may be more appropriate. In the next section, we will explore t-SNE in detail and compare it with PCA.
🔍 t-Distributed Stochastic Neighbor Embedding (t-SNE)
t-Distributed Stochastic Neighbor Embedding (t-SNE) is a non-linear dimensionality reduction technique that is particularly well-suited for visualizing high-dimensional data in two or three dimensions. Unlike PCA, which focuses on preserving global variance, t-SNE focuses on preserving the local structure of the data. This makes t-SNE ideal for identifying clusters and patterns in the data.
t-SNE works by modeling the pairwise similarities between data points in the high-dimensional space and the low-dimensional space. It uses a probability distribution to represent the similarities in the high-dimensional space and a Student-t distribution to represent the similarities in the low-dimensional space. The algorithm then minimizes the divergence between these two distributions using gradient descent. This process ensures that similar points in the high-dimensional space remain close together in the low-dimensional space, while dissimilar points are pushed apart.
One of the key advantages of t-SNE is its ability to reveal the underlying structure of the data. It is particularly effective at visualizing clusters and patterns, making it a popular choice for exploratory data analysis. However, t-SNE has some limitations. It is computationally expensive and may not scale well to large datasets. Additionally, t-SNE is stochastic, meaning that different runs of the algorithm may produce different results. This makes it less suitable for tasks that require reproducible results.
Despite its limitations, t-SNE has been successfully applied in various fields. For example, in bioinformatics, t-SNE is used to visualize gene expression data and identify cell types. In natural language processing, t-SNE is used to visualize word embeddings and identify semantic relationships. In computer vision, t-SNE is used to visualize image features and identify patterns. By revealing the local structure of the data, t-SNE helps to uncover hidden patterns and relationships.
In summary, t-SNE is a powerful non-linear dimensionality reduction technique that is well-suited for visualizing high-dimensional data. It is particularly effective at identifying clusters and patterns, making it a popular choice for exploratory data analysis. However, for tasks that require computational efficiency and reproducibility, other techniques like PCA may be more appropriate. In the next section, we will compare PCA and t-SNE in detail.
📊 Comparison of PCA and t-SNE
| Aspect | PCA | t-SNE |
|---|---|---|
| Type | Linear | Non-linear |
| Preserves | Global variance | Local structure |
| Computational Cost | Low | High |
| Scalability | Scales well to large datasets | Less scalable |
| Reproducibility | Deterministic | Stochastic |
| Use Case | Feature extraction, noise reduction | Data visualization, clustering |
🔧 Applications of PCA and t-SNE
PCA and t-SNE have a wide range of applications in various fields. PCA is commonly used for tasks like feature extraction, noise reduction, and data compression. It is particularly useful in image processing, where it is used for face recognition and image compression. In bioinformatics, PCA is used to analyze gene expression data and identify patterns. In finance, PCA is used for risk management and portfolio optimization.
t-SNE, on the other hand, is primarily used for data visualization and exploratory data analysis. It is particularly effective at visualizing high-dimensional data in two or three dimensions, making it a popular choice for identifying clusters and patterns. In bioinformatics, t-SNE is used to visualize gene expression data and identify cell types. In natural language processing, t-SNE is used to visualize word embeddings and identify semantic relationships. In computer vision, t-SNE is used to visualize image features and identify patterns.
Both PCA and t-SNE have their unique strengths and weaknesses, making them suitable for different tasks. PCA is more suitable for tasks that require computational efficiency and reproducibility, while t-SNE is more suitable for tasks that require data visualization and exploratory analysis. By understanding the differences between these two techniques, data scientists can choose the right tool for their specific needs.
🎯 Quiz on Dimensionality Reduction
❓ Frequently Asked Questions
1. What is the difference between PCA and t-SNE?
PCA is a linear dimensionality reduction technique that preserves global variance, while t-SNE is a non-linear technique that preserves local structure.
2. When should I use PCA?
PCA is suitable for tasks that require computational efficiency, feature extraction, and noise reduction.
3. When should I use t-SNE?
t-SNE is ideal for visualizing high-dimensional data and identifying clusters or patterns.
4. Is PCA deterministic?
Yes, PCA is deterministic and produces the same results for a given dataset.
5. Is t-SNE suitable for large datasets?
No, t-SNE is computationally expensive and may not scale well to large datasets.