Basics of Probability for Data Science

🎉 Basics of Probability for Data Science

Probability is a branch of mathematics that studies the likelihood of events occurring. It plays a crucial role in data science by providing the framework for making informed predictions based on observed data. In data science, we rely on probability to assess the uncertainty in models, to evaluate risks, and to make data-driven decisions. Understanding probability lays the foundation for further explorations into statistical modeling, machine learning, and decision-making processes.

The essence of probability can be observed in everyday life; whether it's weather forecasting, stock market predictions, gaming strategies, or marketing analytics, probability seamlessly integrates into various domains. This post aims to dissect the basics of probability as it pertains to data science, covering various types of probabilities, key concepts such as probability distributions, and practical applications. Understanding these concepts is vital for data scientists who seek to leverage data for analytics, modeling, and informed predictions.

As we delve deeper into the subject, we'll explore fundamental probability concepts including experiments, outcomes, and events. We'll differentiate between theoretical versus empirical probability and examine how these aspects manifest in data science scenarios. Additionally, we will look at how understanding probabilities enables data scientists to conduct hypothesis testing, build machine learning models, and perform A/B testing effectively.

This extensive guide provides a comprehensive overview for beginners and serves as a valuable resource for experienced data scientists looking to refresh their understanding of probability. By the end of this post, readers will be equipped with foundational knowledge and practical insights essential for harnessing the power of probability in their data science endeavors.

Let's embark on this exploratory journey to understand the basics of probability for data science! 🚀

📌 Probability Fundamentals

At its core, probability quantifies uncertainty. The probability of an event is defined as a measure of the likelihood that the event will occur, expressed as a number between 0 and 1. A probability of 0 indicates that the event will not occur, while 1 indicates that it will certainly happen. The mathematical representation of probability can be expressed formally as:

P(Event) = (Number of favorable outcomes) / (Total number of outcomes)

In probability theory, some fundamental concepts include experiments, outcomes, and events. An experiment is a procedure that yields one or more results. An outcome is a specific result of an experiment, while an event is a collection of outcomes. Understanding these elements is essential for analyzing complex data scenarios.

For instance, consider the simple experiment of rolling a single die. The possible outcomes are the numbers 1 through 6, and the event of rolling an even number includes the outcomes {2, 4, 6}. The probability of this event is calculated as:

P(Even Number) = 3/6 = 0.5

This groundwork facilitates comprehension as we progress into more complex probability concepts such as conditional probability, independence, and the application of Bayes' theorem.

🧮 Types of Probability

Probability can be classified into several types, each serving distinct functions in mathematical modeling and analysis. The primary categories of probability are:

1. Theoretical Probability

Theoretical probability is determined through logical analysis and is often derived from a known set of conditions. It assumes that all outcomes in a sample space are equally likely.

2. Experimental Probability

Experimental probability refers to the probability derived from conducting experiments. It is calculated by dividing the number of times an event occurs by the total number of trials conducted. This type supports empirical validation of theoretical concepts.

3. Subjective Probability

Subjective probability (or personal probability) is based on personal judgment and beliefs regarding the likelihood of an event occurring. It is more qualitative and less mathematically rigorous than the other types.

The contextual application of different probability types is vital; for example, while theoretical probability may suffice for simple random scenarios, experimental probability becomes crucial in complex environments such as A/B testing in data science, where outcomes can be influenced by varying external factors.

📊 Probability Distributions

Probability distributions describe the likelihood of obtaining the possible values of a random variable. They can be discrete (finite or countable outcomes) or continuous (infinite outcomes). Two of the most widely used distributions in data science include:

1. Discrete Probability Distributions

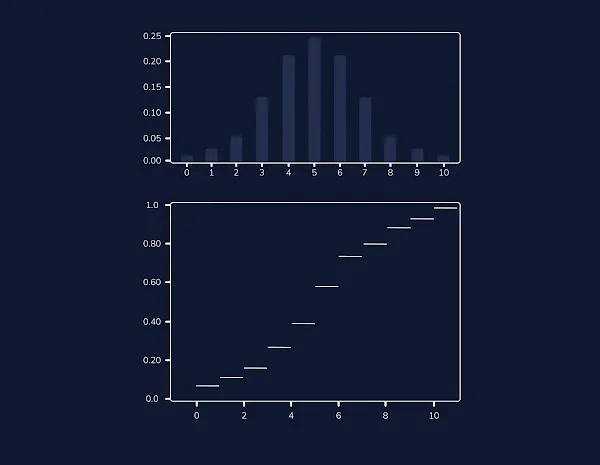
The discrete probability distribution defines the probabilities of the outcomes of a discrete random variable. A common example is the Binomial Distribution, which models the number of successes in a fixed number of independent Bernoulli trials.

2. Continuous Probability Distributions

Continuous probability distributions apply to continuous random variables and are used to model scenarios where outcomes can take on an infinite number of values within a certain interval. The Normal Distribution (bell curve) is a key example often used in statistics and is characterized by its mean and standard deviation.

Understanding these distributions underpins many data science methodologies, especially in predictive modeling and hypothesis testing. For example, when assuming normally distributed data, statistical conclusions can be drawn using confidence intervals and significance tests.

🔍 Applications in Data Science

Probability plays a critical role in multiple domains within data science. Here are some prominent applications:

1. Machine Learning

In machine learning, probability is foundational. Many algorithms, such as Naïve Bayes classifiers, use probabilistic models to make predictions based on input data. Understanding underlying probabilities allows data scientists to assess model performances and craft effective strategies.

2. A/B Testing

A/B testing is a statistical method used to compare two versions of a webpage or product to determine which one performs better. Probability allows for calculating the likelihood that observed differences between groups are statistically significant.

3. Risk Analysis

In business and finance, leveraging probability helps identify potential risks and their impacts. Probabilistic models enable decision-makers to evaluate strategies and optimize returns while minimizing threats.

Overall, mastering these probability applications enhances a data scientist's ability to extract insights, make predictions, and engage stakeholders with data-driven arguments.

🧩 Data Puzzle Challenge!

Puzzle 1:

If a card is drawn from a standard deck of 52 playing cards, what is the probability that it is an Ace?

Puzzle 2:

If a six-sided die is rolled, what is the probability of rolling a number greater than 4?

Puzzle 3:

In a class of 30 students, 10 are female. What is the probability of randomly selecting a female student?

Puzzle 4:

Two coins are tossed. What is the probability of getting at least one head?

Puzzle 5:

a bag contains 6 red balls and 4 blue balls. What is the probability of randomly selecting a red ball?

❓ Frequently Asked Questions

1. What is the difference between independent and dependent events?

Independent events are those whose outcomes do not affect each other, while dependent events are those where the outcome of one event affects the outcome of another.

2. How can I apply probability in data science?

Probability is applied in various ways such as in machine learning algorithms, A/B testing, data analysis, and risk assessment.

3. What is Bayes' Theorem?

Bayes' Theorem is a mathematical formula used to calculate conditional probabilities, allowing for the revision of predicted probabilities based on new evidence.

4. How do I interpret a p-value?

A p-value indicates the probability of obtaining an observed result given that the null hypothesis is true. A lower p-value suggests stronger evidence against the null hypothesis.

5. Is probability the same as chance?

Probability is a quantifiable measure of the likelihood of an event occurring, whereas chance is more qualitative and often used informally to describe the likelihood of events.